When it comes to statistical analysis, two prominent schools of thought have dominated the field for decades: the frequentist and Bayesian approaches. Each has its philosophy, principles, and techniques. In this blog post, we'll explore the key differences between these approaches, provide practical examples, discuss their use cases, and include code snippets to help you grasp the distinctions.

Frequentist Approach:

Core Principle: Frequentist statistics is based on the frequency of events in repeated, independent experiments. Probability is seen as the long-term relative frequency of an event.

No Prior Knowledge: Frequentist methods typically do not incorporate prior knowledge or subjective beliefs. They rely solely on the data at hand.

Interpretation: Frequentist statistics provide point estimates and confidence intervals. It does not provide a probability distribution for the parameters; instead, it focuses on the probability distribution of the observed data.

Use Cases: Frequentist methods are commonly used in large sample sizes, traditional experimental designs, and situations where prior information is either unavailable or deemed irrelevant.

Frequentist Statistics: The Realm of Objective Observations

Philosophy*:* Frequentist statistics is grounded in the concept of objective, observable data. It argues that probabilities should be based solely on observed frequencies and that inferences are derived from the long-run behaviour of events.

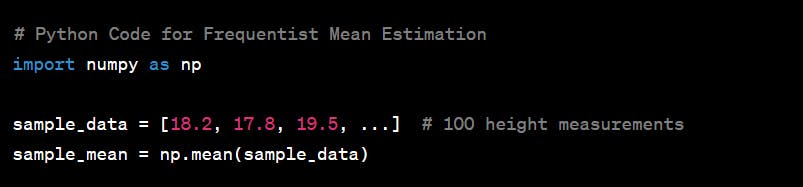
Practical Example*:* Suppose you want to estimate the average height of a certain tree species in a forest. You measure the heights of 100 randomly selected trees and calculate the sample mean as your point estimate of the population mean.

Bayesian Approach:

Core Principle: Bayesian statistics is grounded in probability theory. It treats probability as a measure of belief or confidence in an event occurring.

Prior Knowledge: A key feature of Bayesian analysis is the incorporation of prior knowledge or beliefs about a situation. This prior knowledge is updated with new data to form a posterior distribution.

Interpretation: Bayesian statistics provides a probability distribution for the parameters of interest. This distribution represents the uncertainty about the true values of these parameters given the observed data.

Use Cases: Bayesian methods are particularly useful when dealing with small sample sizes, complex models, and situations where prior information is available and relevant.

Bayesian Statistics: Embracing Subjectivity and Priors

Philosophy*:* Bayesian statistics incorporates subjective probabilities based on prior beliefs. It views probabilities as degrees of belief and uses Bayes' theorem to update these beliefs with new data.

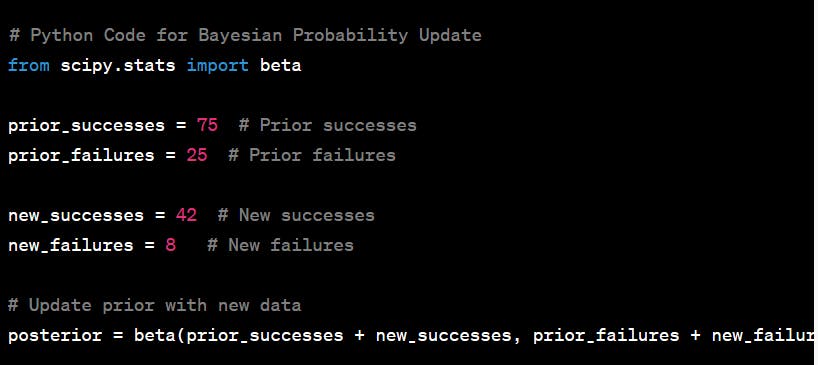
Practical Example*:* Imagine you want to estimate the probability of success in a clinical trial for a new drug. You have prior data suggesting a success rate of 75%, and you collect new trial data to update your estimate.

Practical Use Cases:

1. Frequentist Approach:

   • Hypothesis testing, e.g., A/B testing in website optimization.

   • Confidence intervals for parameter estimation.

   • Large-scale data analysis where frequentist methods provide stable results.

2. Bayesian Approach:

   • Personalized medicine: Tailoring treatments based on individual patient data.

   • Rare event modelling: Assessing low-frequency events with limited data.

   • Incorporating expert opinions and prior knowledge.

Comparing the Approaches:

• Frequentist statistics is often considered more suitable for traditional, objective scenarios with ample data.

• Bayesian statistics excels in situations with limited data, uncertainty, and the need to incorporate prior knowledge.

Choosing Between Bayesian and Frequentist:

1. Data and Sample Size: Bayesian methods can be advantageous with smaller sample sizes or when dealing with complex models. Frequentist methods are often preferred in large-sample settings.

2. Prior Information: If you have relevant prior information or expert knowledge, Bayesian methods allow you to incorporate this into your analysis. Frequentist methods are generally agnostic to prior information.

3. Interpretability: If you need a probability distribution for your parameters and want to directly interpret probabilities, Bayesian methods might be more suitable. If you're focused on point estimates and frequentist confidence intervals, the frequentist approach might be preferred.

4. Complexity of the Model: Bayesian methods can handle complex models with more flexibility. If your analysis involves intricate modeling, Bayesian methods might offer advantages.

5. Tradition and Convention: Sometimes the choice between Bayesian and Frequentist methods is influenced by tradition, conventions in the field, or personal preferences.

In summary, frequentist and Bayesian statistics offer distinct approaches to statistical analysis, each with its strengths and use cases. It's not a matter of one being universally better than the other but rather a consideration of which approach aligns better with the goals of the analysis. Understanding the differences and choosing the right approach depends on the nature of the problem and the available data.

#DataPills #DataDose #DataBytes #DataAnalysis #DataScience #Statistics #BayesianVsFrequentist